|
Aufgabe I: |
Gegeben sind die Standard-Elektrodenpotenziale
für Cu/Cu2+:
+0,35V,
Au/Au3+:
+1,42 V
und 2Cl¯/Cl2:
+1,36 V |
|
Arbeitsaufträge
Lösungen:
|
1. |
Berechne die Elektrodenpotenziale für alle drei
Systeme bei Ionenkonzentrationen von 0,5 mol/L und 0,0005 mol/L.
Differenziere deine Berechnungen nach folgenden Methoden:
Zur Erinnerung: Kathode ist der
 - Pol oder die Zelle mit der
größeren
Ionenkonzentration.
- Pol oder die Zelle mit der
größeren
Ionenkonzentration.
Für das System Cu/Cu2+ = +0,35V gibt es zwei
Lösungen:
Lösung 1: c(Cu2+) = 0,5 mol/L ==> Reduktionsseite,
+Pol, Kathode
Lösung 2: c(Cu2+) = 0,0005 mol/L. ==> Oxidationssseite, -Pol, Anode.
Methode A: Zunächst ist das Potenzial jeder
einzelnen Halbzelle zu berechnen, also der mit der
Konzentration c(Men+) = 0,5 mol/L und der mit
0,0005 mol/L. Danach wird die Differenz gebildet:
ΔE
= E(Kathode) - E(Anode) = E°Akz
- E°Don
EAkzeptor = E° + 0,059/2 V * lg {c(Cu2+)}
= 0,35 V + 0,059/2 * lg(0,5) = 0,35 V +
0,059/2*(-0,3010) = 0,3411 V
= E-Akzeptor, Kathode, +Pol,
Reduktionselektrode
In der Zelle mit der konzentrierten Lösung werden Metallionen
reduziert, damit Ionen
aus der Lösung gehen und deren Konzentration sich verringert.
EDonator = E° + 0,059/2 V * lg {c(Cu2+)}
= 0,35 V + 0,059/2 * lg(0,0005) = 0,35 V +
0,059/2*(-3,3010) = 0,2526 V
= E-Donator, Anode, - Pol,
Oxidationselektrode
In der Zelle mit der verdünnten Lösung werden die Metallatome
oxidiert, damit
Ionen in die Lösung hineingehen und deren Konzentration sich vergrößert.
Differenz der Potenziale:
U = ΔE = EKath
- EAn = EAkz - EDon = 0,3411 V - 0,2526 V
= 0,0885 V
Methode B:
Die Nernst-Gleichung wird aufgestellt und umformuliert,
dann erst die Werte eingesetzt.
Da Akzeptor- und Donator-Halbzelle das selbe Standardpotenzial
haben E° haben, kann
es aus der Beziehung U = ΔE
= EKath - EAn auch herausgerechnet werden.
Damit gilt:
U = ΔE = 0,059/2 V
* lg {cKath(Cu2+)/cAn(Cu2+)}
= 0,059/2 V * lg {0,5 mol/L /0,0005mol/L}
= 0,059/2 V * lg {1000} = 0,059/2 V*
3
DE
= 0,0885 V
|
|
2. |
Vergleich der
Werte bei beiden Methoden:
Bei beiden Methoden kommt dasselbe Ergebnis heraus.
Fazit:
Für Redoxsysteme, bei denen es sich in der Donator-
und Akzeptor-Halbzelle um dieselbe Metall-/Metallionen-Kombination
handelt, kann das Standardpotenzial aus der Gleich eliminiert
werden. Es gilt die Nernst-Gleichung in der Form:
ΔE
= 0,059/n V * lg {cKath(Men+)/cAn(Men+)}
= 0,059/n V * lg
{c(konz.Lsg) /
c(verd.Lsg)}
= 0,059/n V * lg {c(Akz) /
c(Don)}
= 0,059/n V * lg {c(Oxidation) / c(Reduktion)}
Für Au/Au3+
mit E° = 1,42 V und
c(konz) = 0,5 mol/L und c(verd) = 0,0005 mol/L gilt:
ΔE = 0,059/n V * lg {cKath(Men+)/cAn(Men+)}
= 0,059/3 V * lg{0,5 mol/L / 0,0005 mol/L}
= 0,059/3 * V * 3
=
0,059 V
Fazit:
Aus dem Vergleich der Cu/Cu2+ - und Au/Au3+-
Systeme wird deutlich: bei Konzentrationszellen mit identischen Ionen
in beiden Halbzellen kommt es auf das Standard-Potenzial nicht an,
lediglich die Konzentrations-Differenz bestimmt das Potenzial des
Gesamtsystems bzw. der Zellen.
Für
2Cl¯/Cl2:
+1,36 V gilt:
E = E° + 0,059/2 V * lg {1/c2(Cl¯)}
= E° - 0,059 V * lg c(Cl¯)}
Reaktionsgleichung: 2 Cl¯ <===> Cl2 (aq) + 2 e¯
E = 0,059/2 V * lg {p(Cl2) / c2(Cl¯)}
Bei Reaktionen, an denen sowohl gasförmige als auch gelöste
Stoffe
beteiligt sind, kann man nebeneinander
die Zahlenwerte der Druckangaben
(in bar) und Konzentrationsangaben in (mol/L) verwenden.
Nach der Allgemeinen Gasgleichung p * v = n * R * T gilt:
p = n/V * R * T und damit
p = c * R * T
Ist p(Cl2) = 1 bar = 105 Pa, dann gilt:
E = E° + R * T
* lg {1/c2(Cl¯)}
= E° - R * T * lg{c(Cl¯)}
2 * M * F
M * F
E = E° + 0,059 V * lg 1
= E° +
0,059 V * (-lg{c2(Cl¯)}
2
{c2(Cl¯)}
2
= E° - 0,059 V * lg{c(Cl¯)}
Anwendung: Für c(Cl¯)
= 0,5 mol/L gilt dann:
Konz. Lsg.=
Anode = Oxidation = Donator
= -Pol
EAn = E° - 0,059V * lg {c(Cl¯)}
= +1,36 V - 0,059 V * (-0,3010) = 1,36 V + 0,0178
V
=
1,3778 V
Für c(Cl¯) =
0,0005 mol/L gilt dann:
Verd. Lsg. =
Kathode = Reduktion = Akzepor =
+Pol
EKath. = E° - 0,059V * lg {c(Cl¯)}
= +1,36 V - 0,059 V * (-3,3010) = 1,36 V + 0,1948
V
=
1,5548 V
Vereinfachung : DE =
0,059/n V * lg {c(Oxidation) / c(Reduktion)}
= 0,059 V * lg (0,5 / 0,0005 )
= 0,059 V * 3
DE =
0,177 V
Fazit: Auch bei Nme-Reaktionen im gleichen
Ionensystem gilt die Nernst-Gleichung
Man beachte den
Vorzeichen-wechsel und den Wegfall der 2!
im Detail:
Anwendung der
Exponentenregel:
negatives Vorzeichen
Anwendung der
Quotientenregel:
Wegfall der 2!
|
|
3. |
|
Unterschiede |
Me <====>
Men+ |
2 NMe¯
<====> NMe2 |
| Konzentrierte Lösung |
E-Akzeptor |
E-Donator |
|
Kathode |
Anode |
|
+-Pol |
-Pol |
|
Reduktion |
Oxidation |
| Verdünnte Lösung |
E-Donator |
E-Akzeptor |
|
Anode |
Kathode |
|
-Pol |
+Pol |
|
Oxidation |
Reduktion |
|
|
|
|
|
Aufgabe
2: |
Eine Halbzelle, bestehend aus verschiedenen Anteilen der
Lösungen von Eisen(II)-sulfat und Eisen(III)-chlorid, in
die eine Pt-Elektrode eingesetzt wird, wird mit einer Zink-Halbzelle
kombiniert, in der die Zn2+-Ionenkonzentration c(Zn2+)
= 0,1 mol/L beträgt. Dabei ist die Konzentration der
Eisen(II)-sulfat-Lösung
doppelt so groß wie die der Eisen(III)-chlorid-Lösung. |
|
Arbeitsauftrag:
Lösungen:
|
Berechne die Zellspannung!
Zusatzinformation: E°(Zn/Zn2+) = - 0,76 V;
E°(Fe/Fe2+) = - 0,41 V; E°(Fe2+/Fe3+)
= +0,77 V
Die Bedingung über die Konzentrationsverhältnisse ist der
Schlüssel zum Verständnis der Aufgabe:
1
* c(Fe2+) = 2 * c(Fe3+)
Zellspannungsberechnung:
Potenzial der Zn/Zn2+-Halbzelle:
E = E° + 0,059/2 V * lg c(Zn2+)
= 0,76 V + 0,059/2 V * lg(0,1)
= - 0,76 V + (-0,0295)V
= - 0,7895 V
Potenzial der Fe2+/Fe3+-Halbzelle:
Red <==>
Ox + n*eG
E = E° + 0,059 V * lg {c(Ox)
/ c(Red)}
Fe2+ Fe3+
= + 0,77 V * lg {c(Fe3+)
/ c(Fe2+)}
E-reich E-arm
Potenzial der Zn/Zn2+-Halbzelle ist der
Oxidationsvorgang = E-Donator, weil negatives Standard-Potenzial!
dem steht gegenüber das Potenzial der Fe2+/Fe3+-Halbzelle
= E-Akzeptor, weil positives Standard-Potenzial!
Wenn Zn der Elektronendonator ist, dann läuft die Reaktion von Fe3+
zu Fe2+: Fe3+ + 1 e¯ —> Fe2+
Dann ist E = E° + 0,059 V * lg (1 / 2) , weil die Bedingung gilt:
1 * c(Fe2+) = 2 * c(Fe3+)
= 0,77 V + ((0,059 V * (-0,3010)) = 0,77 V - 0,0178 V
= 0,7522 V
Dann gilt: U = DE = EKath
- EAn = 0,7522 V - (- 0,7895 V)
= 1,5417 V
|
|
Aufgabe
3: |
Permanganat-Ionen sind in saurer Lösung gute
Oxidationsmittel. |
|
Arbeitsaufträge: |
1. |
Vergleiche die verschiedenen Redoxpotenziale der
Reduktion von Permanganat-Ionen miteinander. |
|
2. |
Begründe, weshalb die Oxidationswirkung einer KMnO4-Lösung
mit geringer werdender H+-Ionenkonzentration abnimmt.
Zusatzinformation:
Redoxpotenziale verschiedener
Permanganat-Reaktionen.
MnO4¯
+ eG
<===> MnO42-
E° = 0,56V
MnO4¯ + 2H2O + 3
e¯ <===>
MnO2(s)
+ 4 OH¯ E° = 0,59 V
MnO4¯
+ 4H+ + 3 e¯
<===> MnO2(s)
+ 2 H2O E°= 1,69 V
MnO4¯
+ 8H+ + 5 e¯
<===> Mn2+
+ 4 H2O
E° = 1,51 V
|
| Lösungen: |
|
Zugrundeliegende Redoxreaktion ist: MnO4¯
+ 8 H+ + 5 e¯ <===>
Mn2+ + 4 H2O
Allgemein:
Ox +
n*e¯ <===>
Red
Anwendung Nernst:
E = E° + 0,059/5 V * lg {c(Ox) / c(Red)}
= E° + 0,059/5 * lg {c(MnO4¯)
* c8(H+) / c(Mn2+)}
E = 1,51 + 0,059/5 * lg {c(MnO4¯)/c(Mn2+)}
+ lg c8(H+)
Anwendung der Produkt-bzw. Quotientenregel und der Definition
-
lg c(H+) = pH
Dann wird: E = E° + 0,059/5 V * lg {c(MnO4¯)/c(Mn2+)}
- 8 * pH}
oder:
= E° + 0,059/5 V * lg {c(MnO4¯)/c(Mn2+)}
-(0,059/5 * 8 * pH)
= E° - 8* 0,059/5 V * pH + 0,059/5 V * lg {c(MnO4¯)/c(Mn2+)}
= 1,51 V - 0,0944 * pH + 0,059/5 V * lg {c(Ox)/c(Red)}
Annahme:
Nimmt
man an, dass c(Ox)/c(Red) = 1 : 1 ist, dann ist 0,059/5 V * lg (1/1) =
0 !
Dann gilt:
E = E° -
0,0944 * pH.
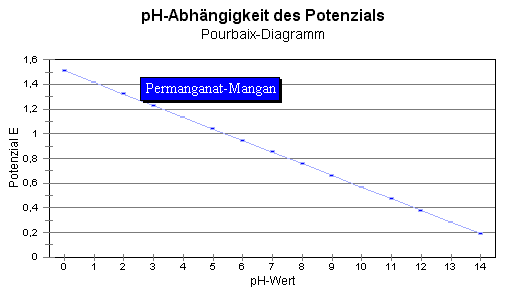
|
Quelle: Tausch/v. Wachtendonk: Chemie SII Stoff-Formel-Umwelt, S. 185 ff,
Bamberg 2004, leicht verändert
Tausch/v. Wachtendonk: Chemie 2000+, Band 2, 35 ff, Bamberg 2004, leicht
verändert
Siehe dazu auch
Beispiele
zur Anwendung der Nernst-Gleichung
(II) im pdf-Format und
Beispiele
zur Anwendung der Nernst-Gleichung
(II) im WordPerfect-Format
update am:
02.02.21
zurück
zur Hauptseite |
